Sumber: https://mafia.mafiaol.com/2014/06/cara-merasionalkan-pecahan-bentuk-akar.html

Cara Merasionalkan Pecahan Bentuk Akar

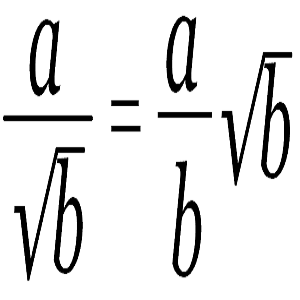
Untuk lebih jelasnya, pelajari uraian berikut.
Merasionalkan Bentuk a/√b Cara merasionalkan bentuk a/√b adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan bentuk sekawan dari penyebutnya, yaitu:

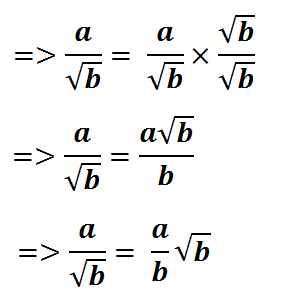
Untuk memantapkan pemahaman Anda tentang cara merasionalkan bentuk a/√b, silahkan simak contoh soal 1 di bawah ini.
Contoh Soal 1 Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah a. 6/√2 b. 10/√5 c. 21/√3 d. 5/√5
Penyelesaian: a.   6/√2 = (6/√2).√2/√2 => 6/√2 = (6√2)/(√2.√2) => 6/√2 = (6√2)/2 => 6/√2 = 3√2
b.   10/√5 = (10/√5).(√5/√5) => 10/√5 = (10√5)/(√5.√5) => 10/√5 = (10√5)/5 => 10/√5 = 2√5
c.   21/√3 = (21/√3).(√3/√3) => 21/√3 = (21√3)/(√3.√3) => 21/√3 = (21√3)/3 => 21/√3 = 7√3)
d.   5/√5 = (5/√5).(√5/√5) => 5/√5 = (5√5)/(√5.√5) => 5/√5 = (5√5)/5 => 5/√5 = √5
Merasionalkan Bentuk a/(b±√c) Cara merasionalkan bentuk a/(b±√c)adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan bentuk sekawan dari penyebut b±√c. Bentuk sekawan dari b + √c adalah b – √c , sedangkan bentuk sekawan dari b – √c adalah b + √c. Berikut penjelasanya masing-masing. Untuk merasionalkan bentuk a/(b+√c), yakni:

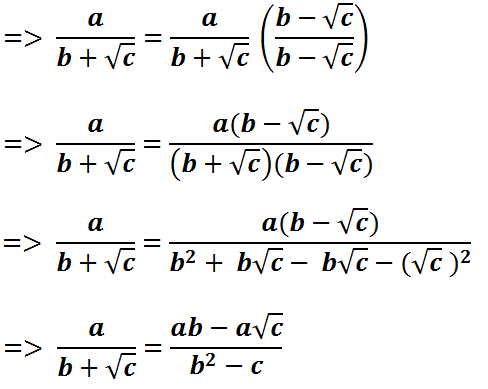
Untuk merasionalkan bentuk a/(b – √c), yakni:

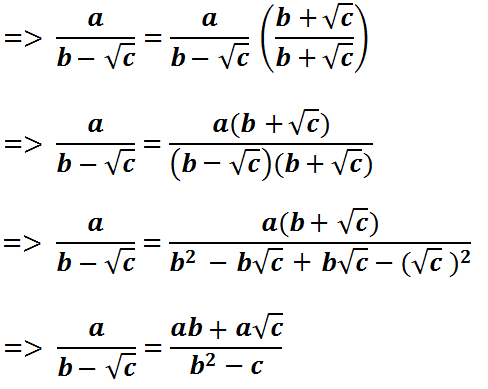
Untuk memantapkan pemahaman Anda tentang cara merasionalkan bentuk a/(b±√c), silahkan simak contoh soal 2 di bawah ini.
Contoh Soal 2 Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah a. 4/(2 + √2) b. 3/(3 – √5) c. 4/(4 + √3) d. 2/(3 – √7) Iklan Penyelesaian: a.   4/(2 + √2) = {4/(2 + √2)}.{(2 – √2)/(2 – √2)} = {4(2 – √2)}/{2 + √2).(2 – √2)} = (8 – 4√2)/(4 – 2) = (8 – 4√2)/2 = 4 – 2√2
b.   2/(2 – √3) = {2/(2 – √3)}.{(2 + √3)/(2 + √3)} = {2(2 + √3)}/{(2 – √3).(2 + √3)} = (4 + 2√3)/(4 – 3) = 4 + 2√3
c.   4/(2 + √5) = {4/(2 + √5)}.{(2 – √5)/(2 – √5)} = {4(2 – √5)}/{(2 + √5).(2 – √5)} = 8 – 4√5)/(4 – 5) = 8 – 4√5)/– 1 = 4√5 – 8
d.   4/(3 – √5) = {4/(3 – √5)}.{(3 + √5)/(3 + √5)} = {4.(3 + √5)}/{(3 + √5)(3 – √5)} = (12 + 4√5)/(9 – 5) = (12 + 4√5)/4 = 3 + √5
Merasionalkan Bentuk a/(√b±√c)

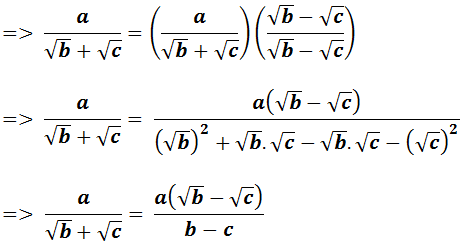
Cara merasionalkan bentuk a/(√b±√c)adalah dengan mengalikan pembilang dan penyebut pecahan tersebut dengan bentuk sekawan dari penyebut √b±√c. Bentuk sekawan dari √b + √c adalah √b – √c , sedangkan bentuk sekawan dari √b – √c adalah √b + √c. Berikut penjelasanya masing-masing. Untuk merasionalkan bentuk a/(√b+√c), yakni:

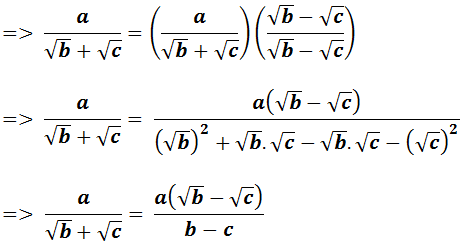
Untuk merasionalkan bentuk a/(√b – √c), yakni:
 
Untuk memantapkan pemahaman Anda tentang cara merasionalkan bentuk a/(√b±√c), silahkan simak contoh soal 3 di bawah ini.
Contoh Soal 3 Rasionalkan penyebut pecahan-pecahan berikut, kemudian sederhanakanlah a. 2/(√3 + √2) b. 3/(√6 – √5) c. 5/(√5 + √3) d. 4/(√11 – √7)
Penyelesaian: a.   2/(√3 + √2) = {2/(√3 + √2)}.{(√3 – √2)/(√3 – √2)} = {2.(√3 – √2)}/{(√3 – √2).(√3 + √2)} = (2√3 – 2√2)/(3 – 2) = 2(√3 – √2)
b. 3/(√6 – √5) = {3/(√6 – √5)}.{(√6 + √5)/(√6 + √5) = {3(√6 + √5)}/{(√6 – √5)(√6 + √5) = 3(√6 + √5)/(6 – 5) = 3(√6 + √5)
c. 4/(√5 + √3) = {4/(√5 + √3)}.{(√5 – √3)/(√5 – √3)} = {4(√5 – √3)}/{(√5 + √3).(√5 – √3)} = 4(√5 – √3)/(5 – 3) = 4(√5 – √3)/2 = 2(√5 – √3)
d. 4/(√11 – √7) = {4/(√11 – √7)}.{(√11 + √7)/(√11 + √7) = {4(√11 + √7)}/{(√11 – √7)(√11 + √7) = 4(√11 + √7)/(11 – 7) = 4(√11 + √7)/4 = √11 + √7